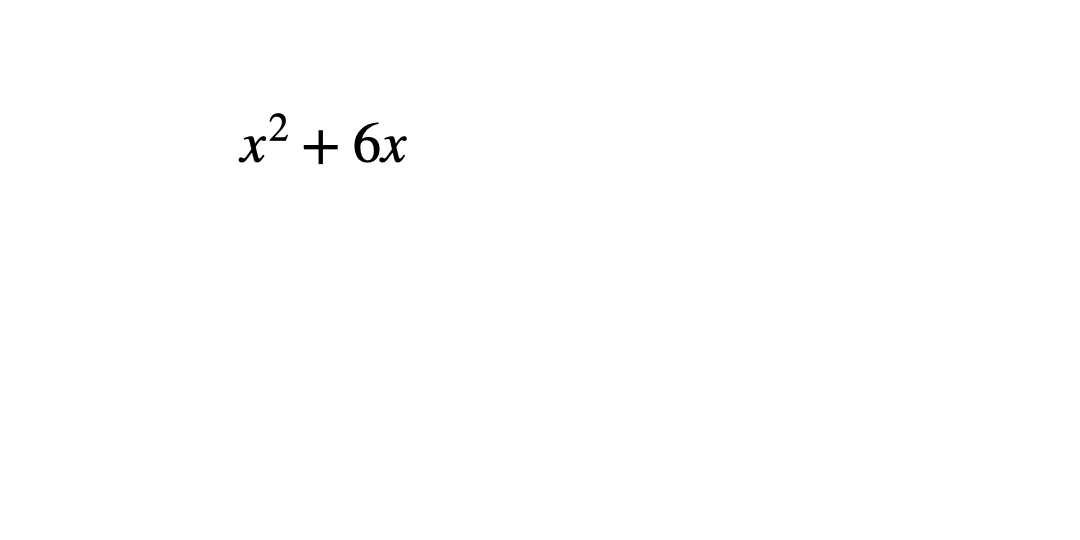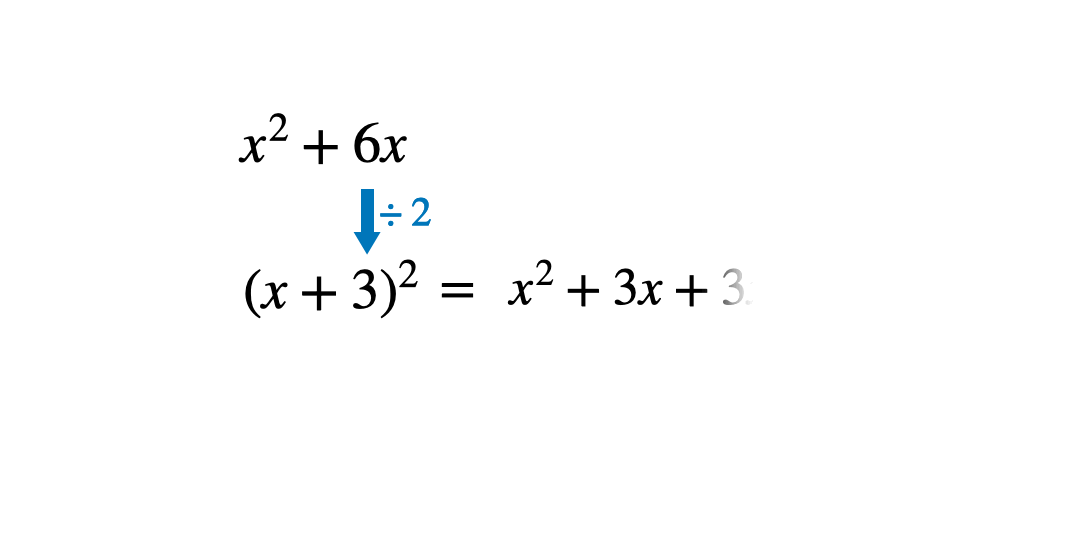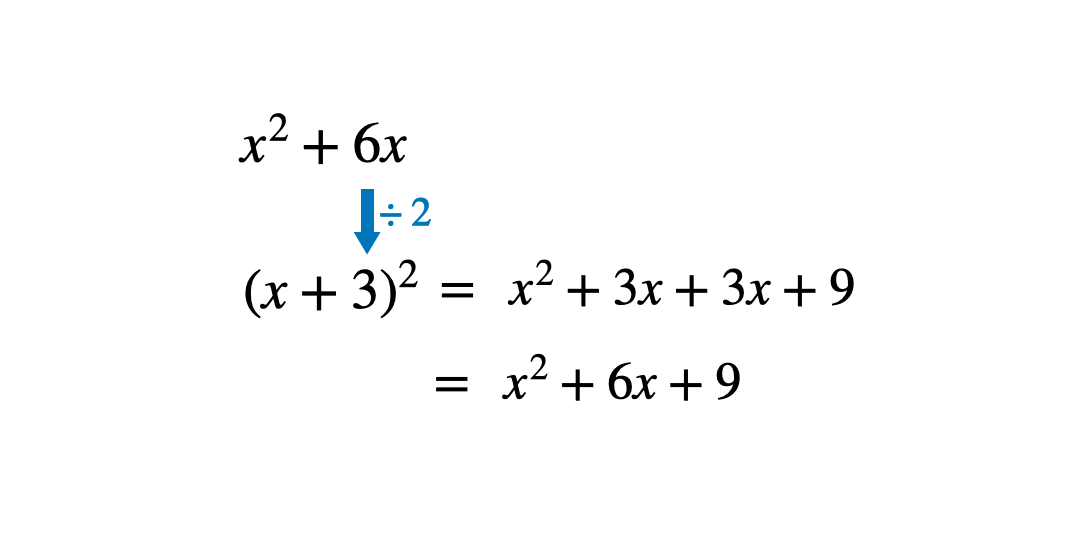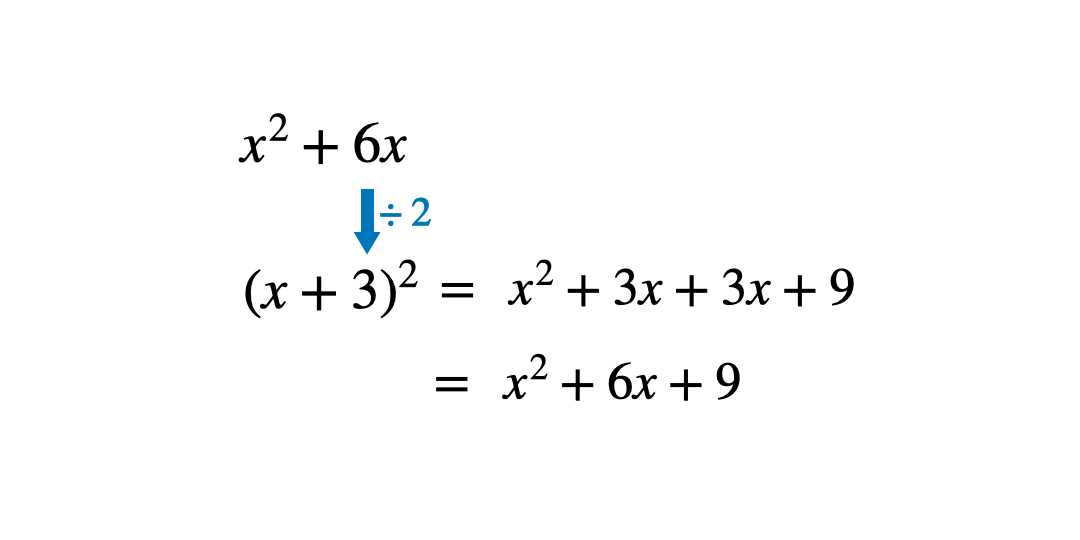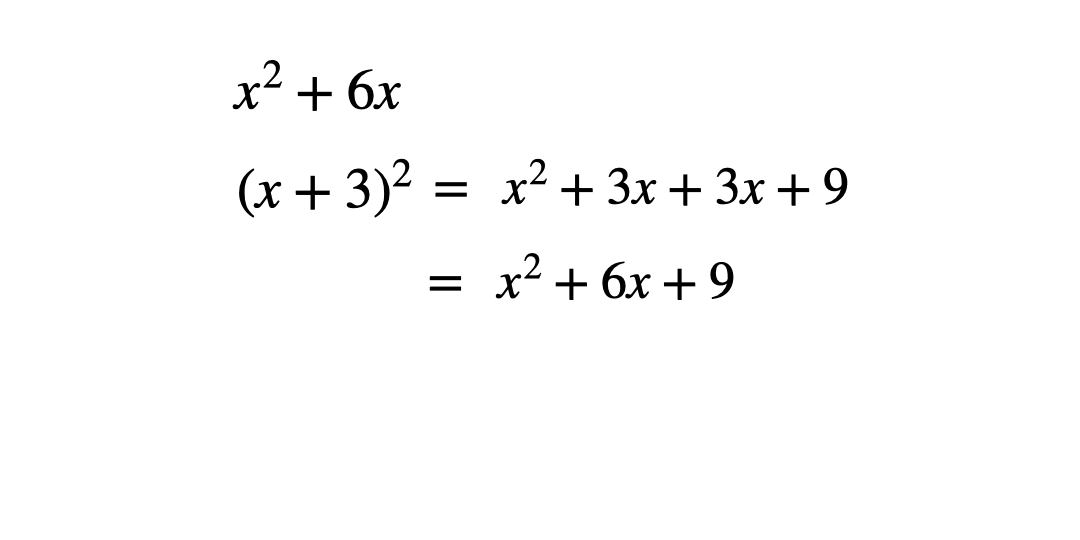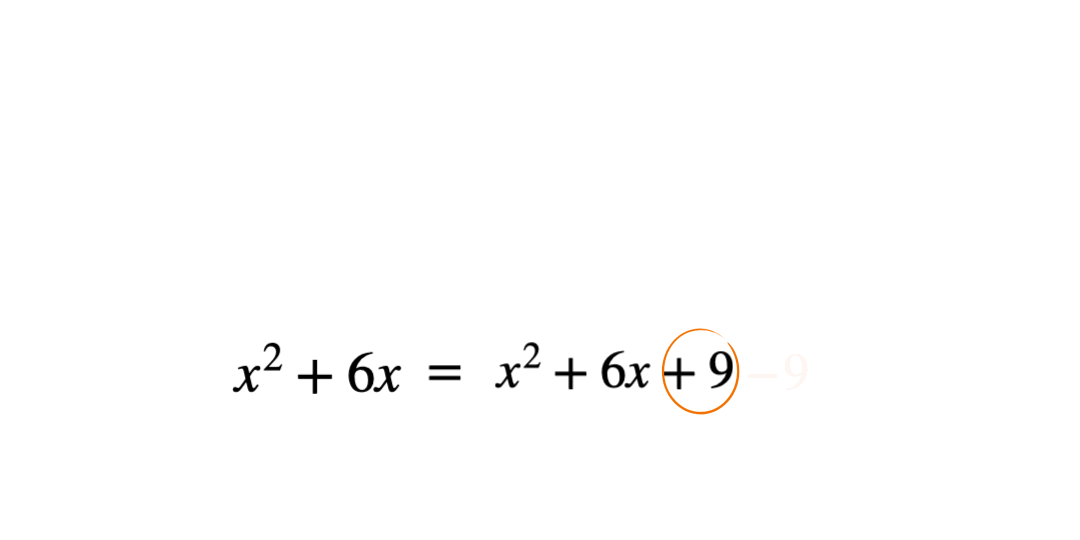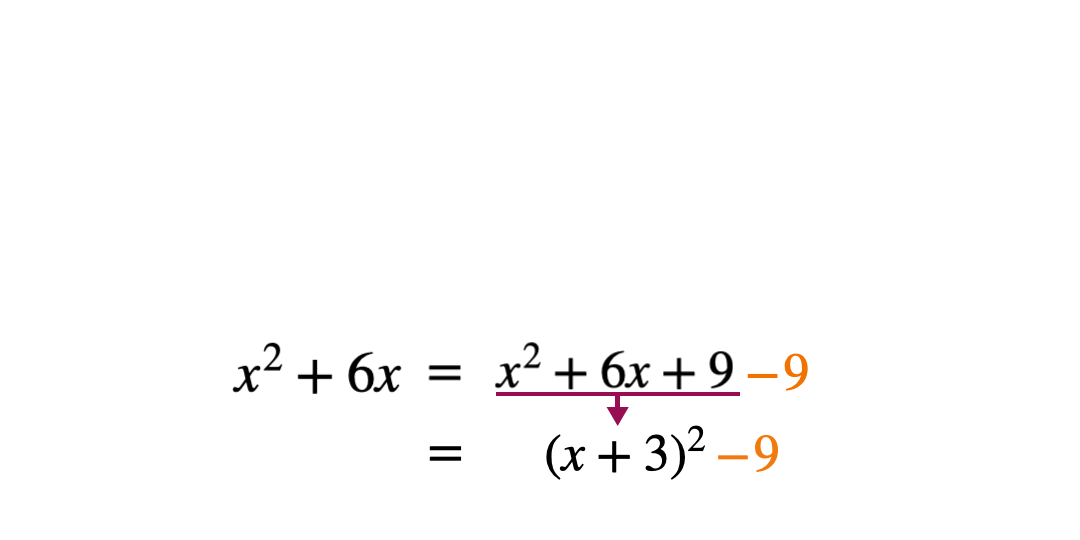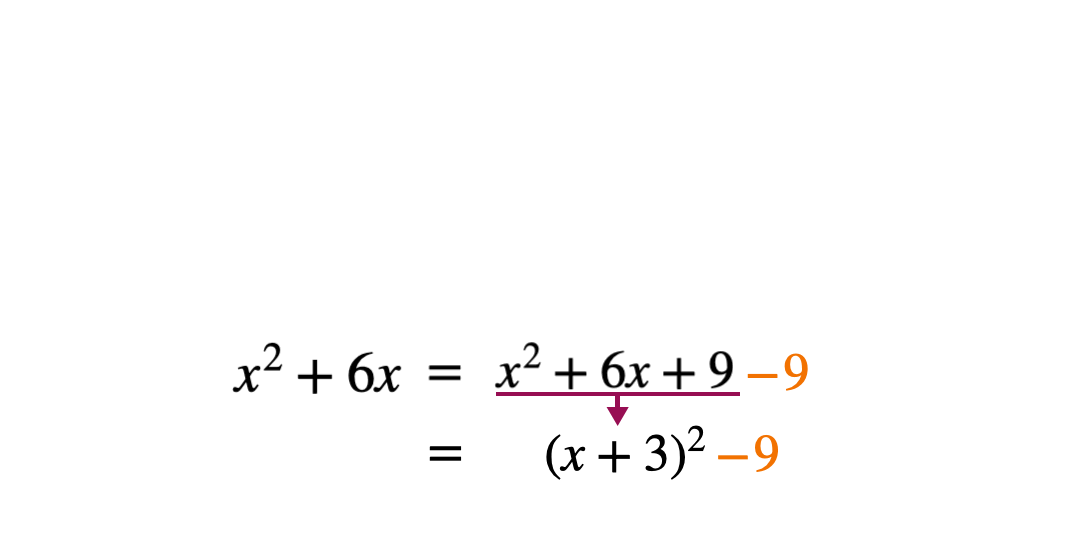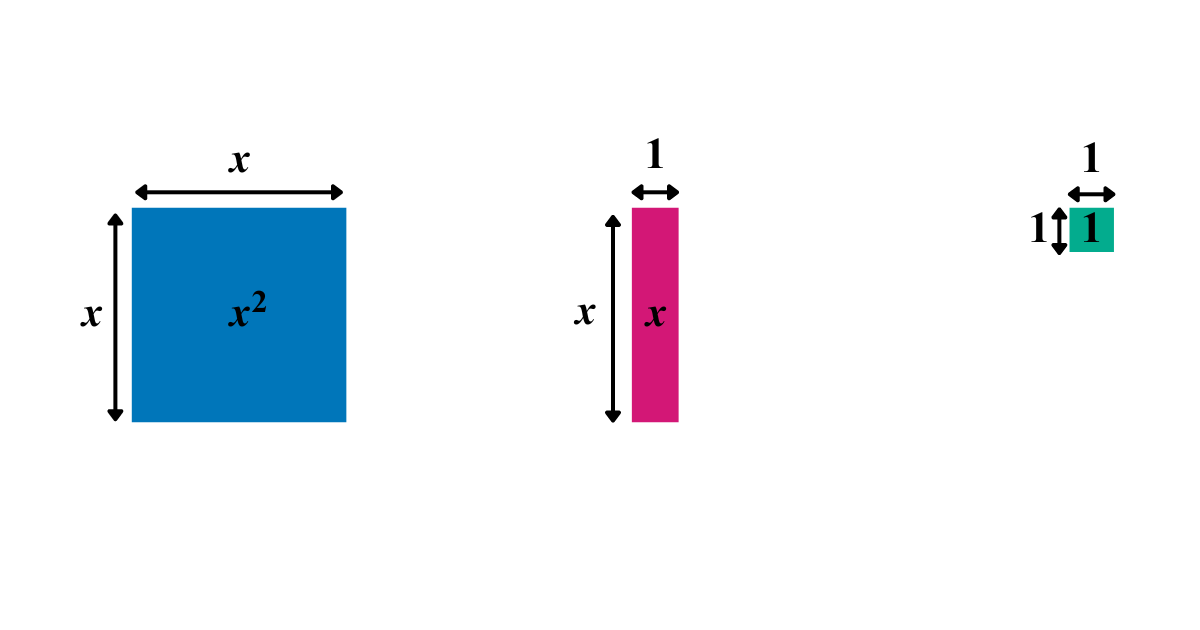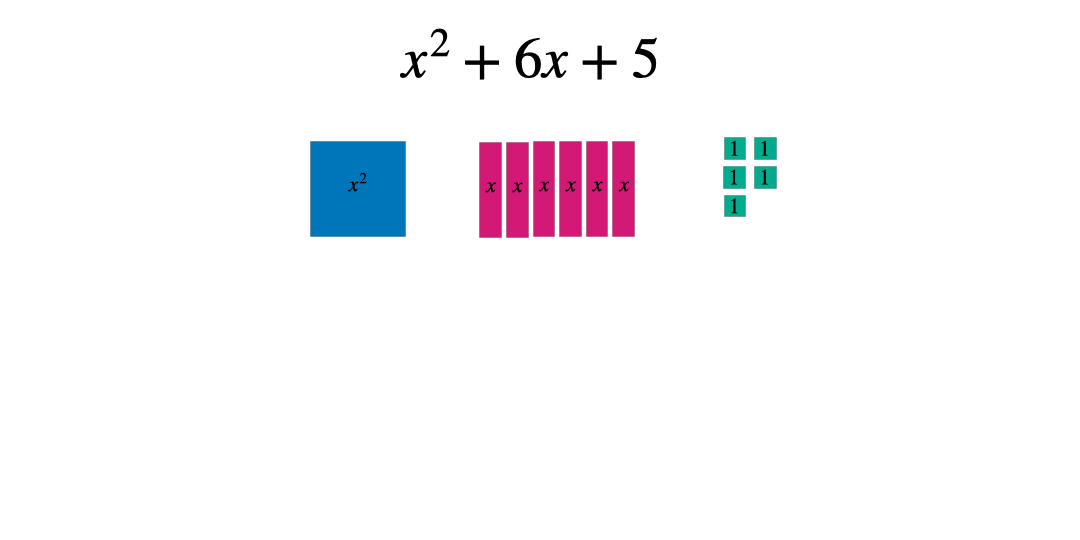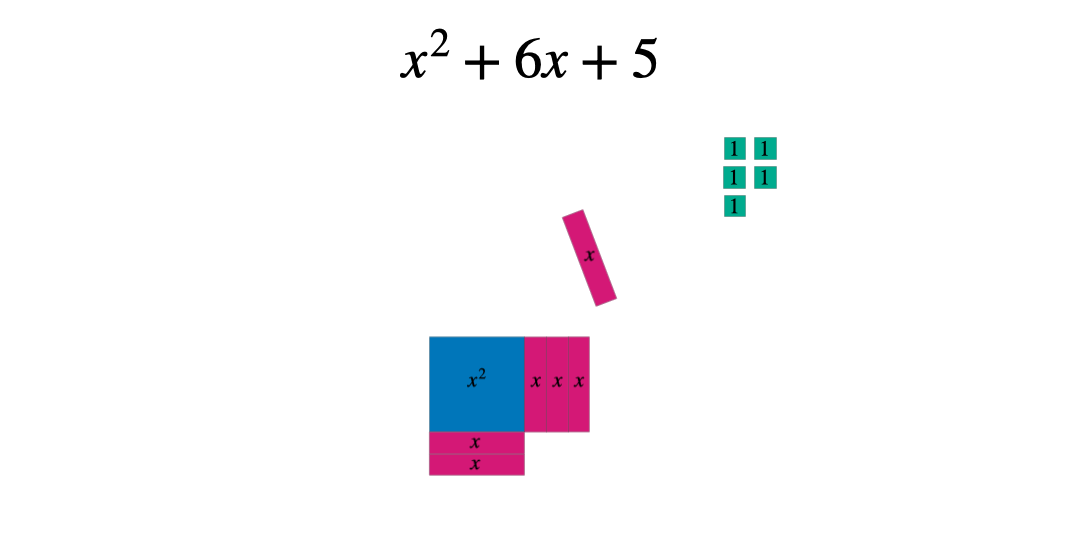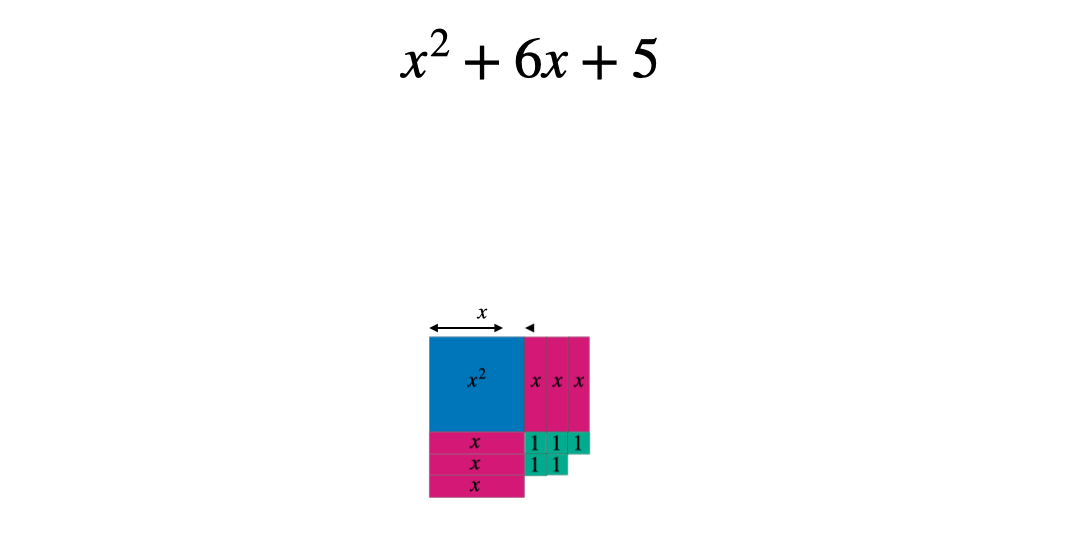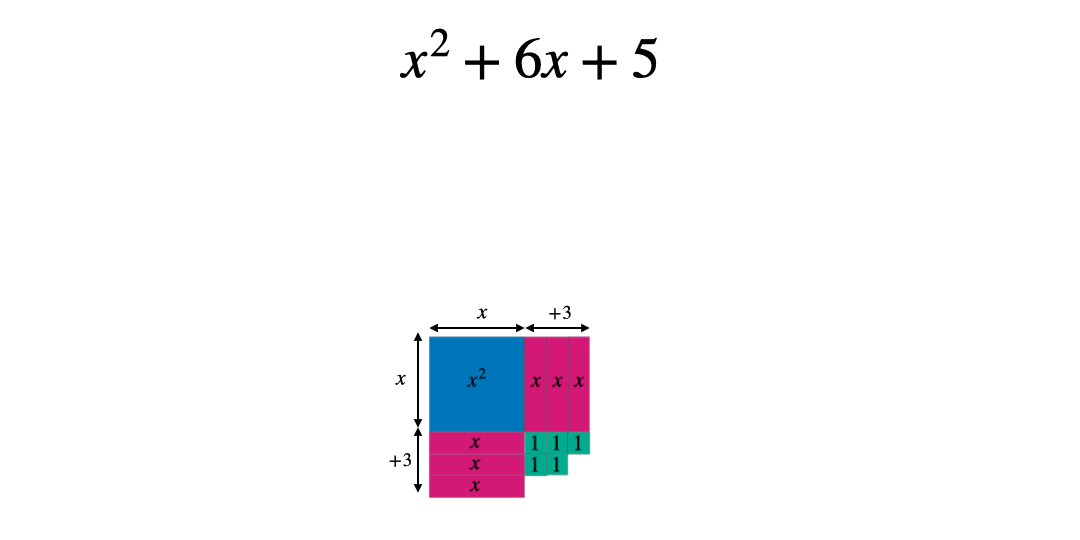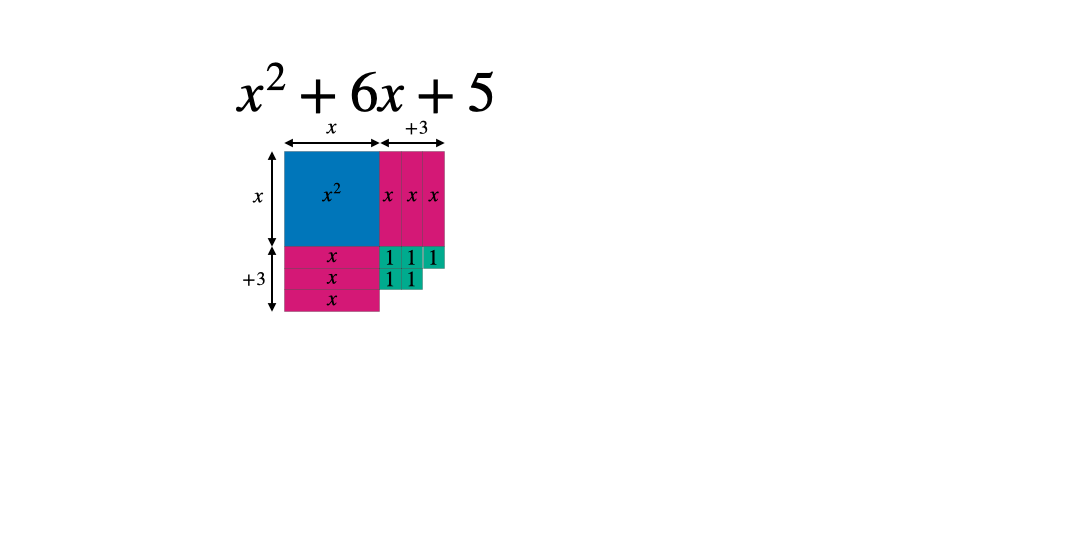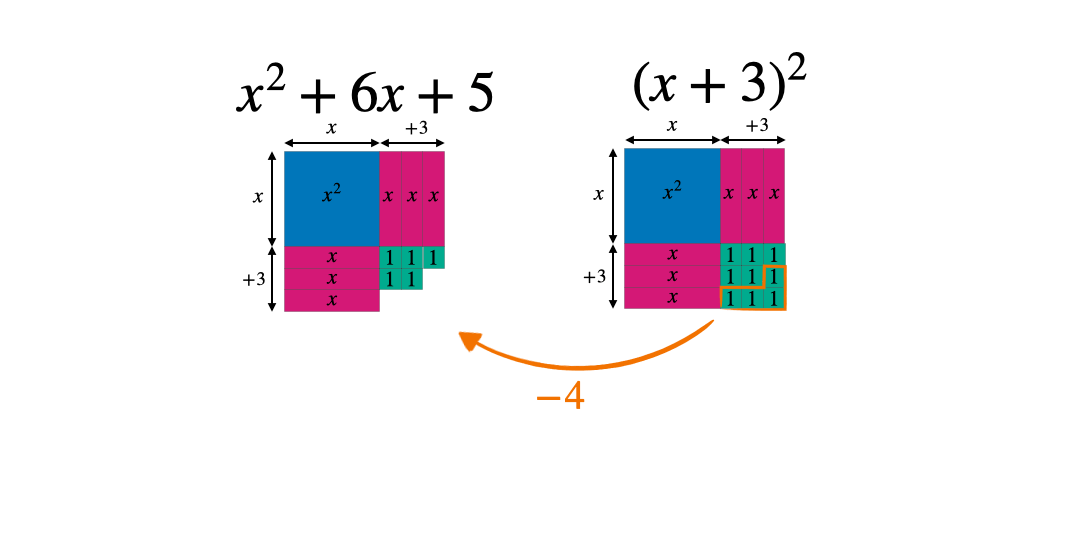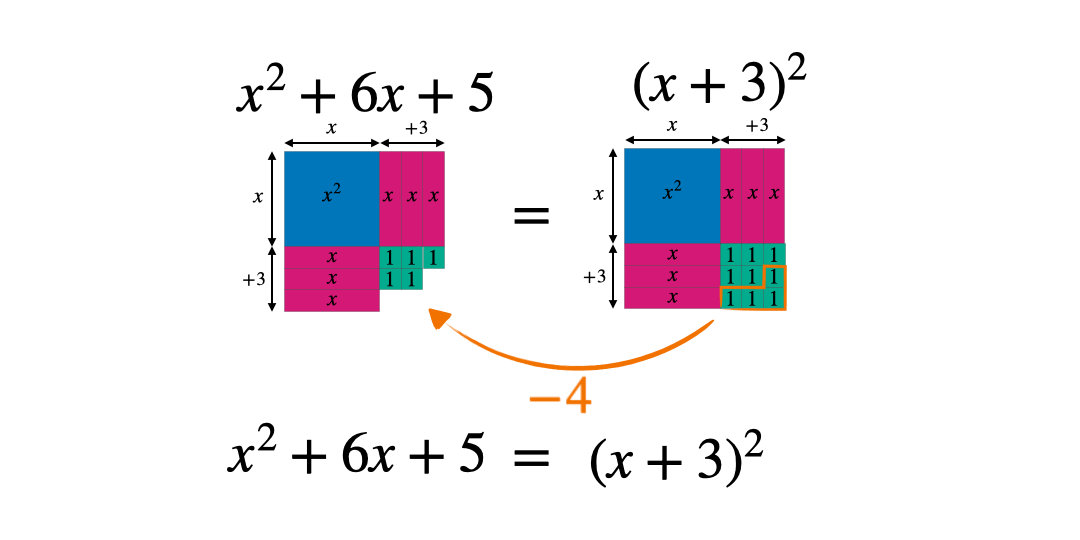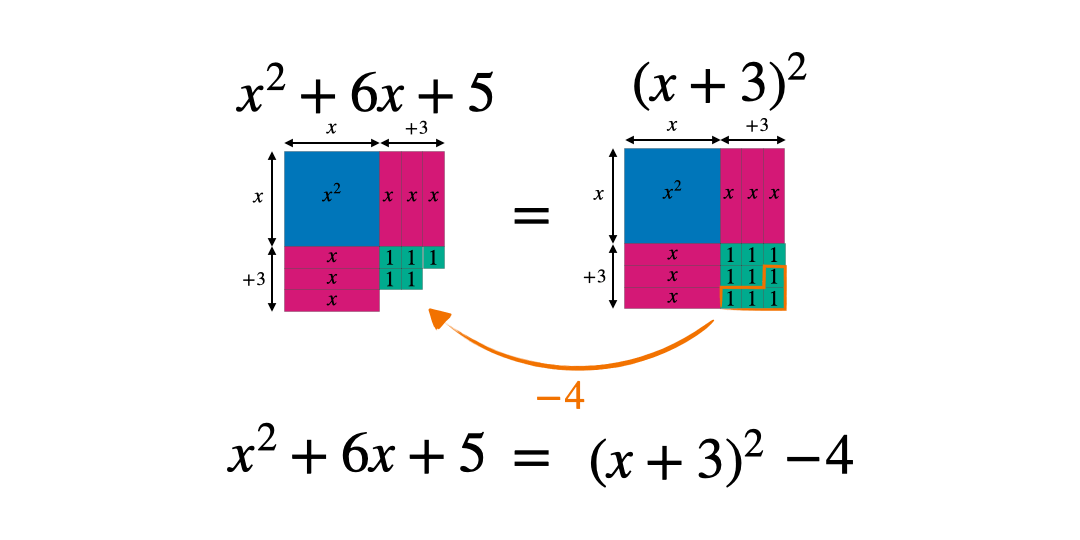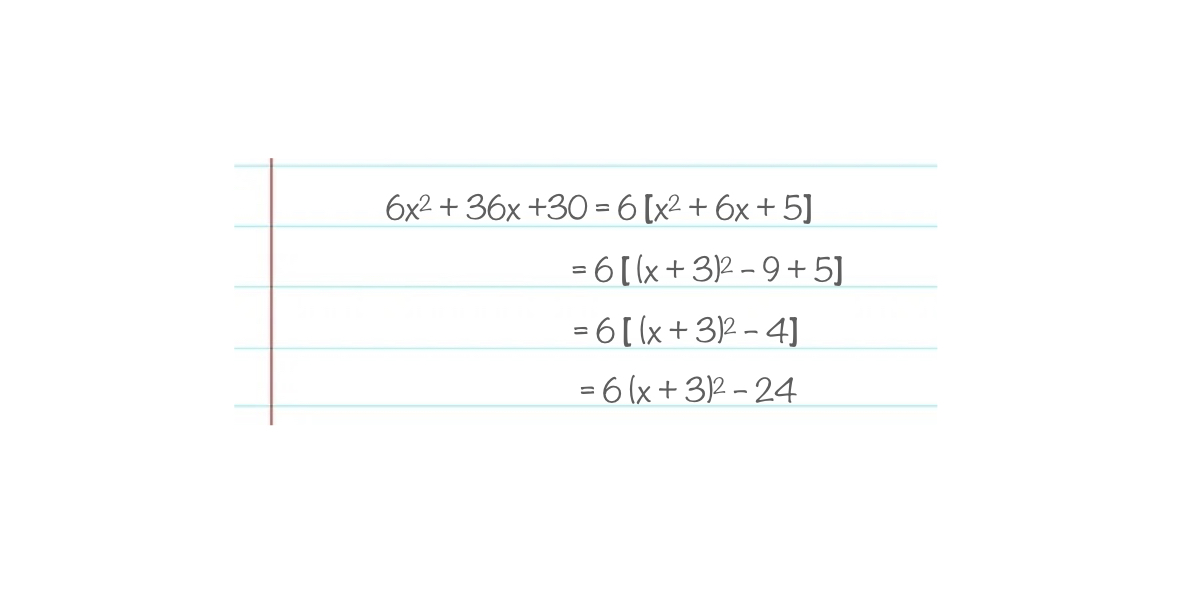Estimated reading time: 8 minutes
Our team of data scientists dived into the CENTURY databanks to find some of the most frequent mistakes made by learners in our secondary maths courses. Then, our team of expert teachers analysed their findings to identify the common misconceptions underlying those errors.
We have written a short series of blogs explaining these misconceptions and suggesting some top tips to address them in the classroom. We hope these will be especially useful for teachers preparing for examinations. This blog is on completing the square. We have also written blogs on the perimeter of compound shapes and rearranging formulae.
Completing the square is an advanced topic assessed at the Higher tier of GCSE and IGCSE. It is an important skill for those wishing to study maths beyond GCSE. Questions can range from those with integer values in the solution to fractions and negatives.
Relevant nuggets:
- Completing the Square 1: (x + q)² + r (MH53.01)
- Completing the Square 2: (x + q/2)² + r (MH53.02)
- Completing the Square 3: p(x + q)² + r (MH53.03)
- Completing the Square 4: –p(x + q/2)² + r (MH53.04)
The simpler questions in the first two nuggets tend to be answered well, with learners answering 72% correctly on average. This drops to 68% in the more complex third nugget, and 60% in the trickiest fourth.
Only 63% of users gave the correct answer of 6(x+3)^2 -24 for this question. Of those who answered incorrectly, the majority had an error in the +q term, most likely resulting from the following misconceptions:
- Not factorising the 6 out of the final term before completing the square
- Not squaring the 3 before subtracting
- Adding the square of 3 rather than subtracting
- Not multiplying by 6 as the final step
The learners who made these mistakes showed some knowledge of completing the square, but it is clear that care needs to be taken when tackling more complex questions where the coefficient of x is not 1. CENTURY’s team of expert maths teachers have put together their top teaching tips to help your students avoid these mistakes when completing the square.
Promote and embed conceptual understanding
When learning how to complete the square, students often know to subtract the square of the constant in the bracket, but many simply remember the process without understanding why. To help build understanding, it can be useful to go back to basics to practise completing the square for an expression with no constant term, for example x2+6x.
Once students have worked out the constant term in the bracket, ask them to expand and simplify this.
When the simplified expanded expression is compared to the original, there is an extra term which is not needed and therefore needs to be subtracted to make the expressions equal. This term is the square of the constant in the bracket.
Use manipulatives so students can visualise the square
Manipulatives are becoming more commonplace in secondary classrooms. These algebra tiles can be a useful tool to help students grasp completing the square using a concrete tool to physically illustrate the values before progressing to the abstract. By considering shapes with the following dimensions and areas students can represent algebraic expressions.
These can then be manipulated to form a square: either with a part missing or some extra pieces. In this case the square has side length x+3 and therefore an area of (x+3)^2 when complete.
Comparing the original expression with the completed square form allows students to see whether they need to add or subtract a constant. The goal is to make the two expressions equal.
Insist on Correct Mathematical Notation
Many of the errors occurred because students did not correctly factorise 6 out of the expression in the first step of working, or they did not correctly multiply by 6 on the last step. Using square brackets when you are modelling solutions to students can be helpful here.
Check by expanding
If students are at a stage in their learning where they are capable of the steps to complete the square, then they also have the necessary skills to check their answer too. Encourage students to expand the brackets and simplify to check they get the original expression. Not only will this help them to spot their own errors - and it is good practice of expanding brackets - it will also help them develop the skills to be a self-moderating learner which is an extremely useful tool for other exams and further study.
We hope that this blog gives you an insight into some of the common challenges learners face when completing the square, and our practical teaching ideas help boost your learners’ confidence and understanding.
Look at the data on your Teacher Dashboard to see if these common misconceptions are present among your learners. Book a demo here.