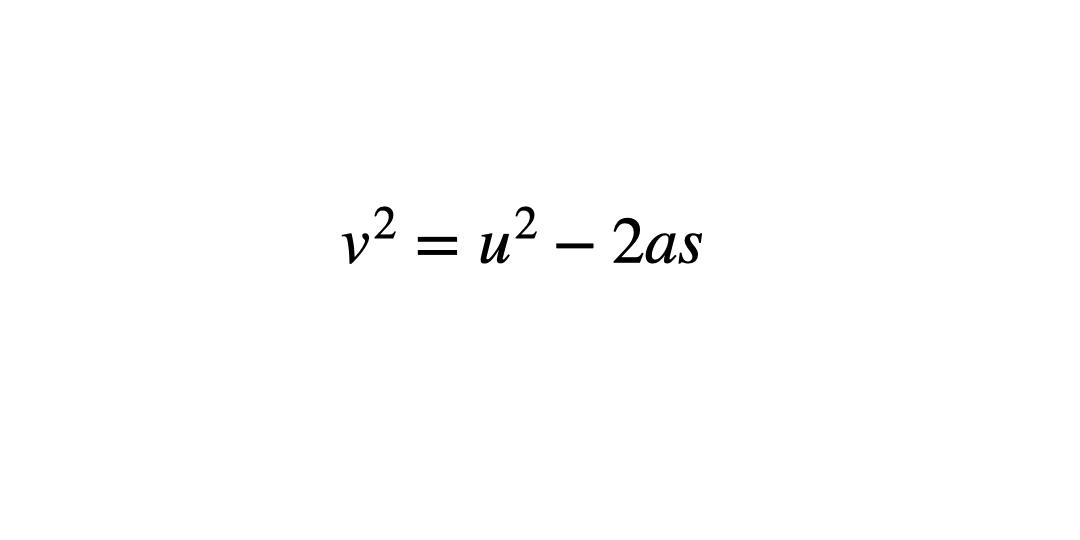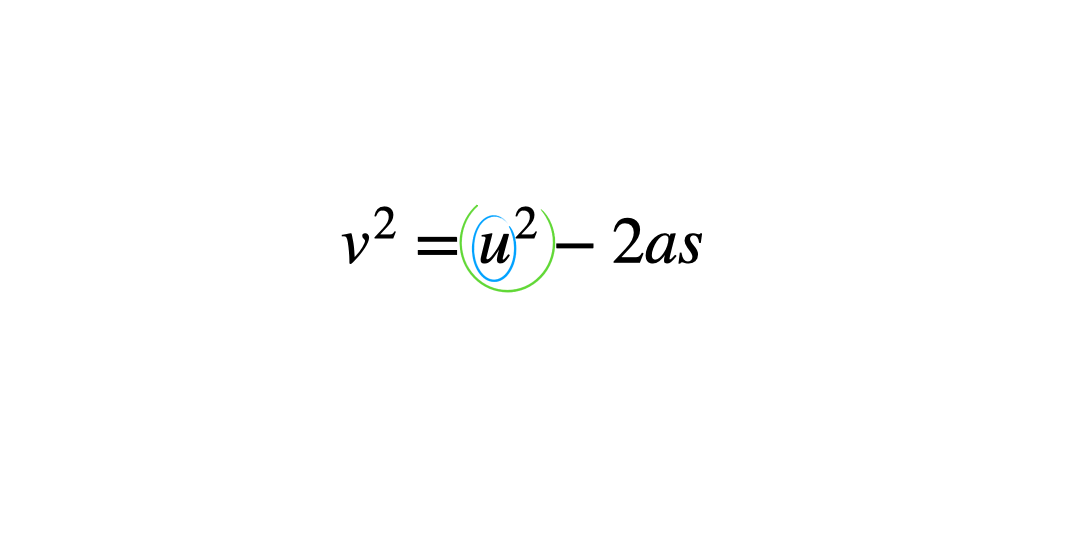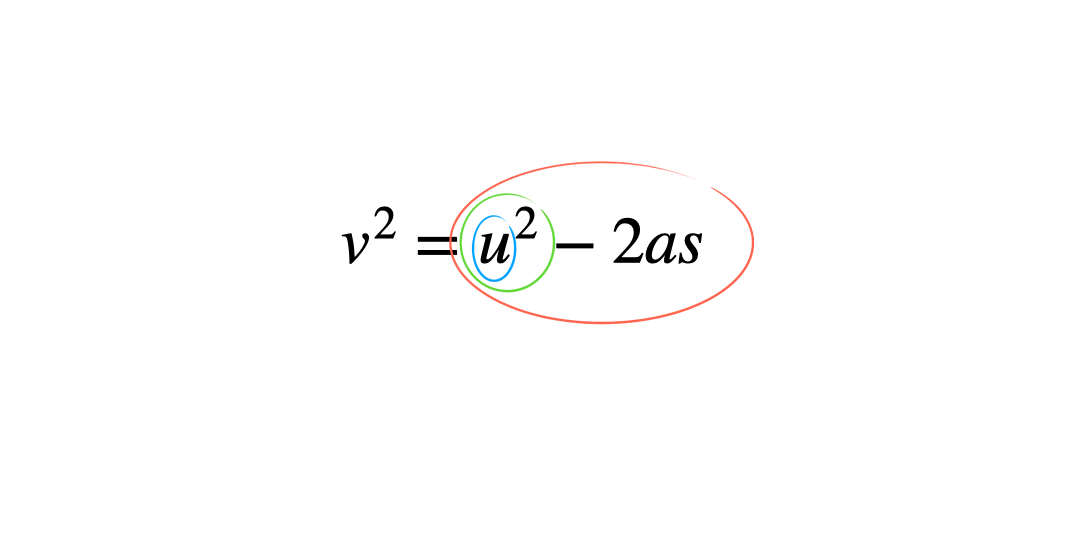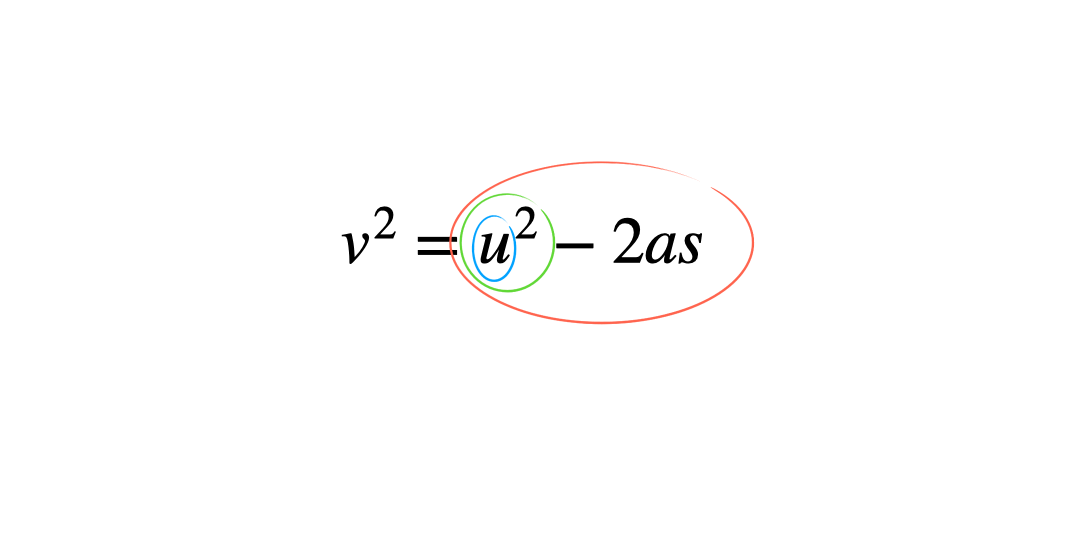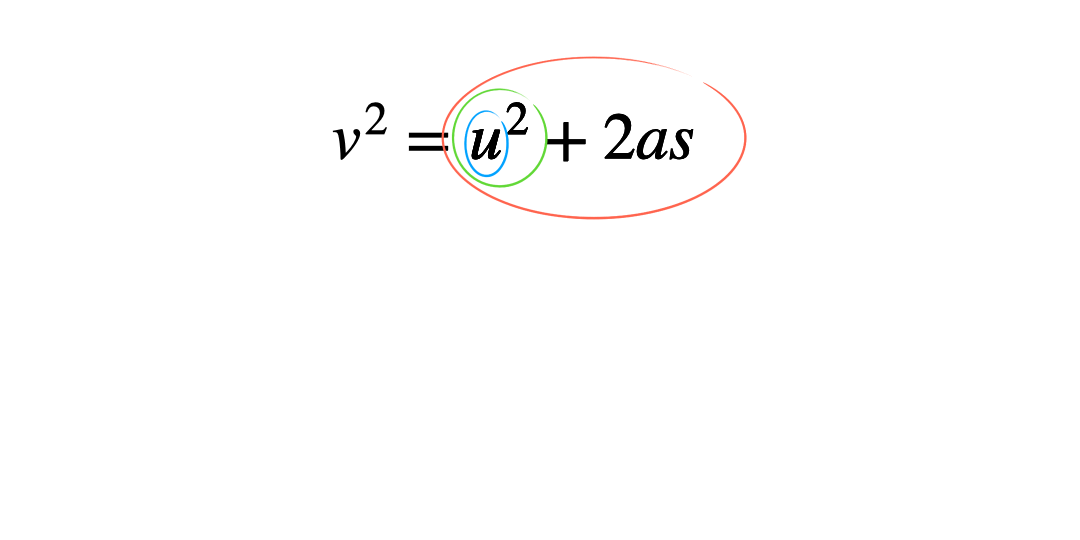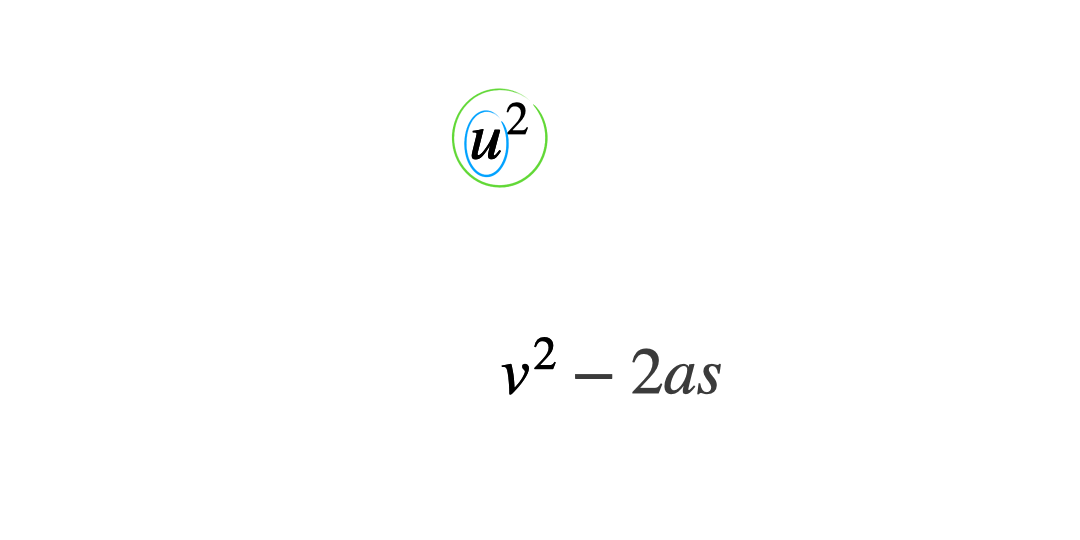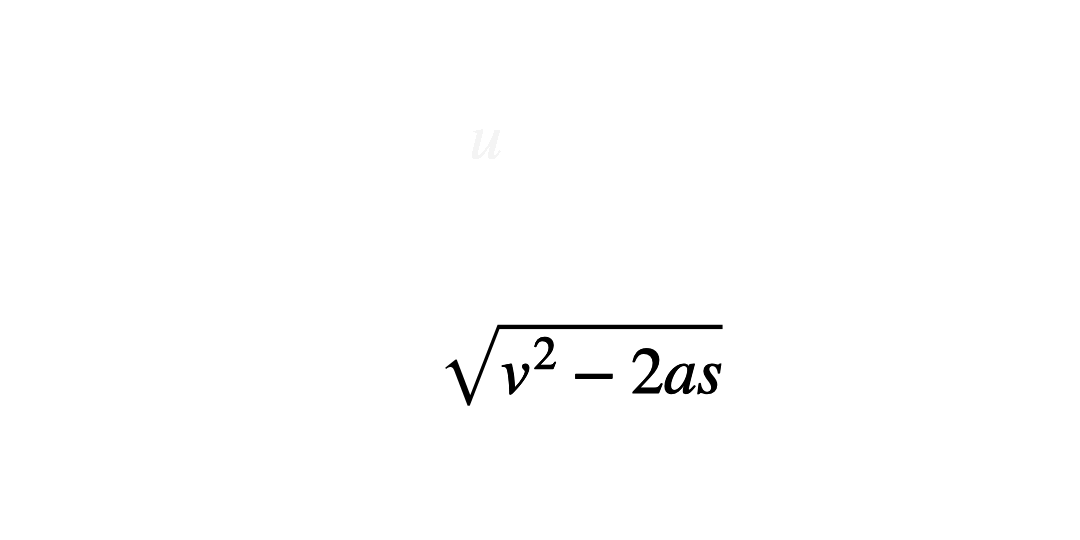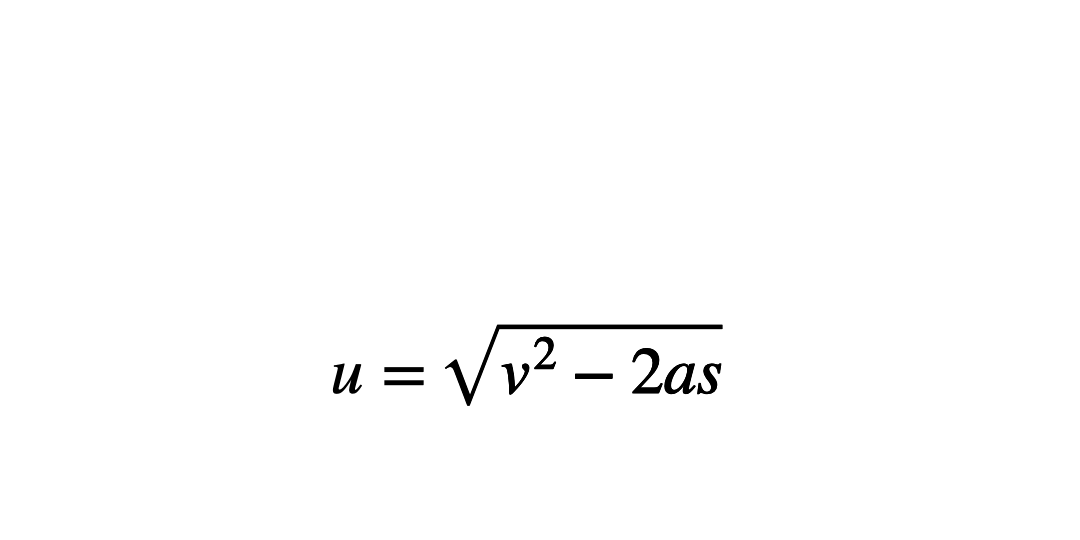Estimated reading time: 6 minutes
Our team of data scientists dived into the CENTURY databanks to find some of the most frequent mistakes made by learners in our secondary maths courses. Then, our team of expert teachers analysed their findings to identify the common misconceptions underlying those errors.
We have written a short series of blogs explaining these misconceptions and suggesting some top tips to address them in the classroom. We hope these will be especially useful for teachers preparing for examinations. This blog is on rearranging formulae. We have also written blogs on the perimeter of compound shapes and completing the square.
Rearranging formulae is assessed at both Foundation and Higher tier of GCSE and IGCSE. Questions can range from simple one-step rearranging to make a given variable the subject, to more advanced rearranging that incorporates skills such as factorising.
Relevant nuggets:
- Rearranging Formulae: One Step (MF21.05)
- Rearranging Formulae: Two Step (MF21.06)
- Rearranging Formulae: Negative Subject (MF21.07)
- Rearranging Formulae: Unknown in Denominator (MF21.08)
- Rearranging Formulae: With Powers (MF21.09)
- Rearranging Formulae: Unknown on Both Sides (MF21.10)
While the simpler questions in this topic had a 68% success rate, this had dropped to only 52% for learners tackling trickier questions involving multiple steps or rearranging and manipulating powers.
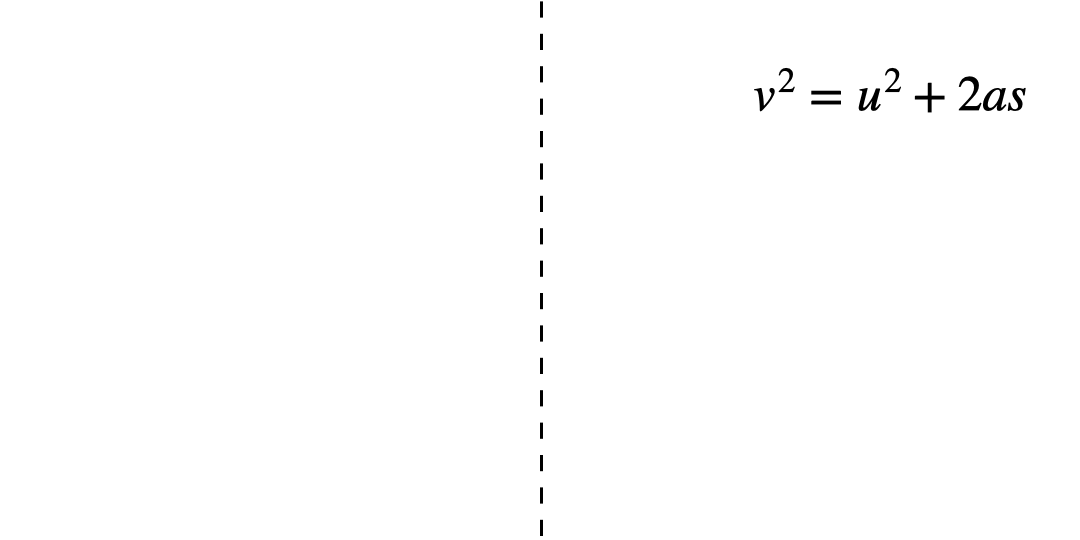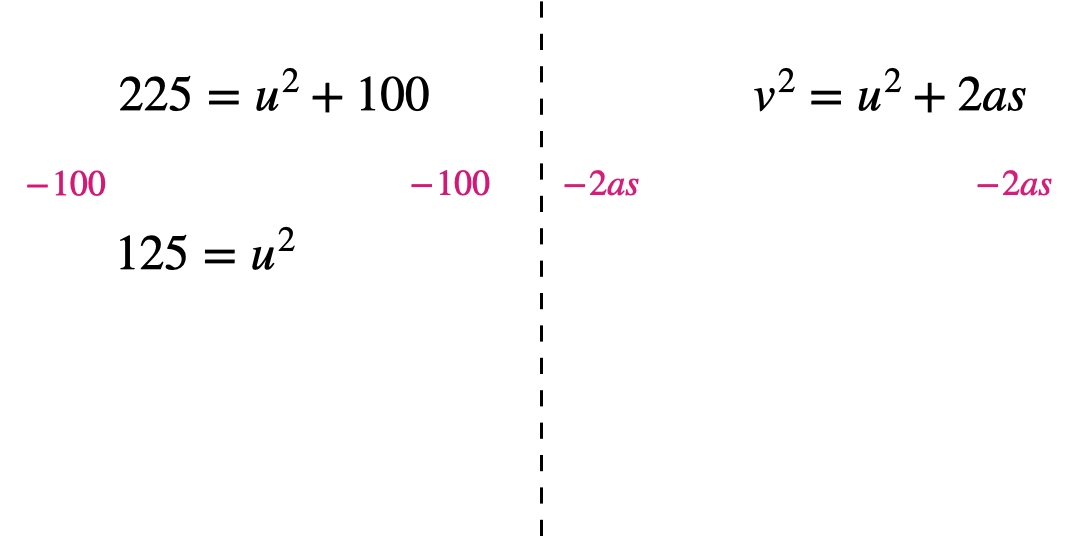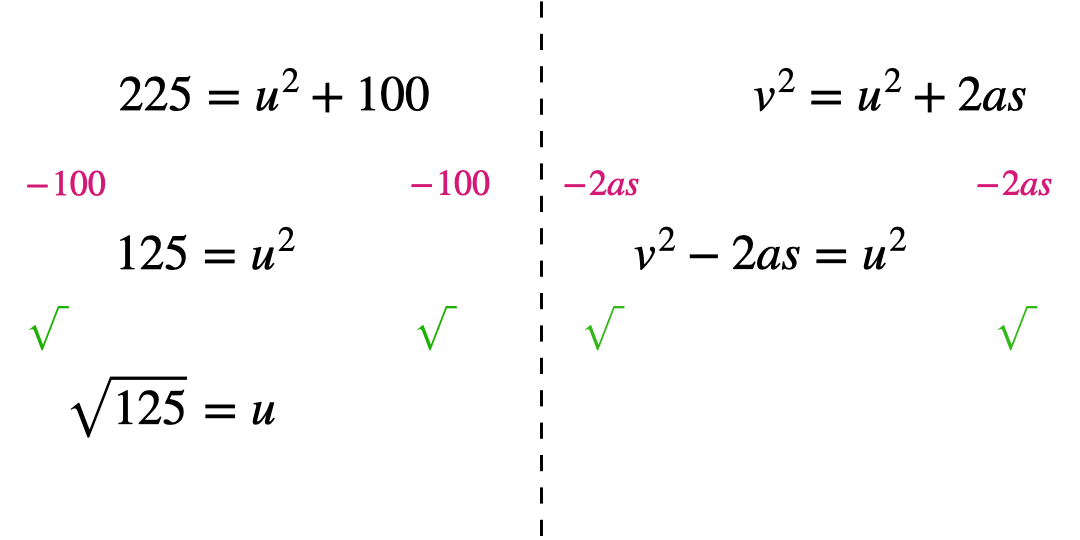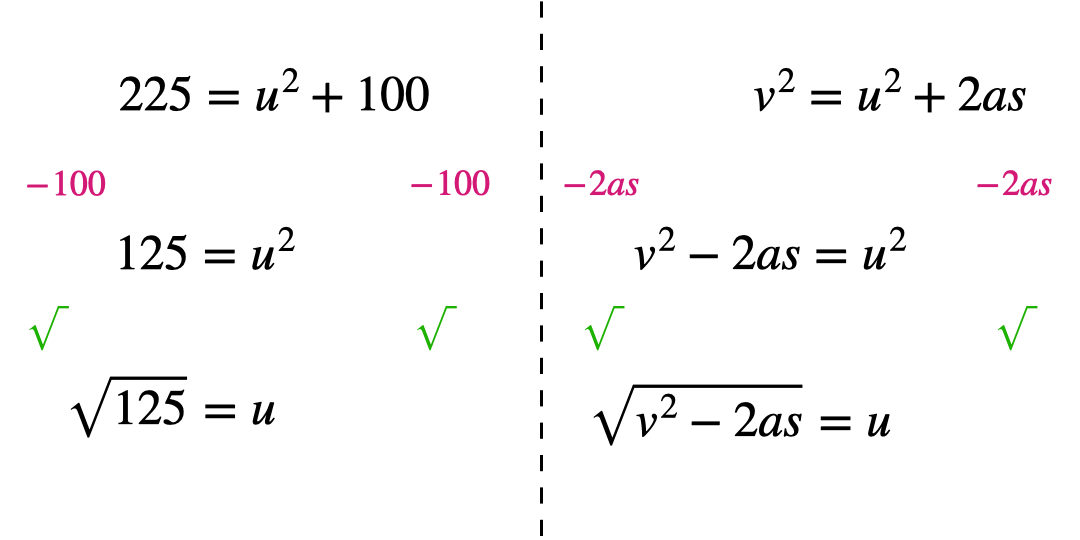
Only 40% of users correctly rearranged this formula. The majority of incorrect answers contained one of the following common misconceptions:
- Not applying inverse operations
- Not applying the inverse operations in the correct order
These students show some understanding of rearranging formulae and inverse operations, but need help implementing these skills correctly in more complex cases. To help students with this topic, CENTURY’s team of expert maths teachers have put together their top teaching tips for rearranging equations. These methods also work well for solving equations.
The ‘onion skin’ method
Circling each operation in ‘layers’ can help students see what order to work through them in. This helps minimise errors which stem from applying inverse operations in the wrong order. Students start by circling the variable to be the new subject and work outwards like the layers of an onion, circling the next operation and so on until the whole operation is enclosed.
To apply this method begin with the original subject of the formula, and then apply the inverse operations in the reverse order.
Replace letters with numbers
Often students are happier solving equations rather than rearranging formulae, even though the underlying knowledge and methods are the same. By creating an equation that matches the formula and working through the steps to solve it, they can apply the same steps to rearrange the formula.
Say it out loud
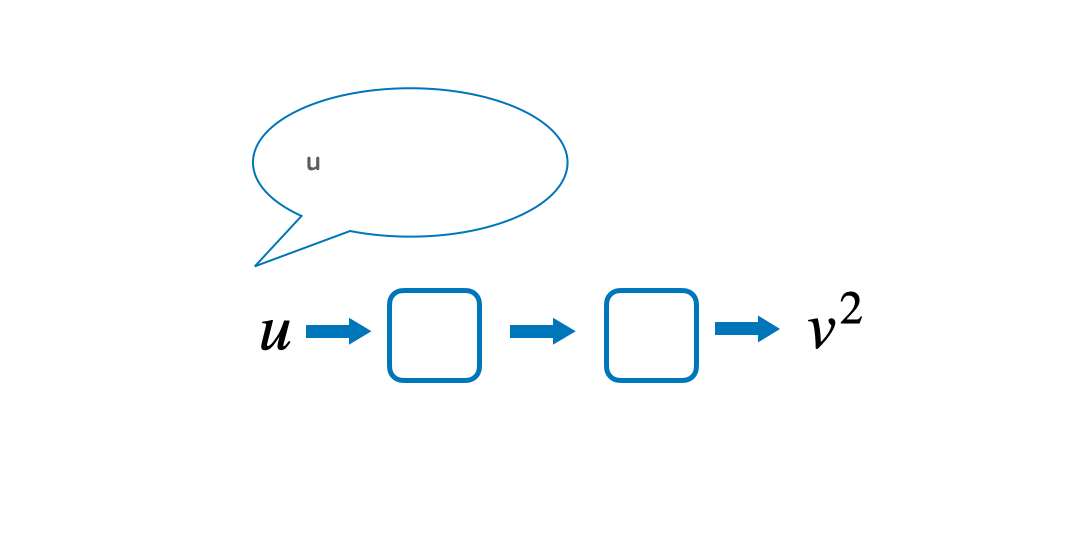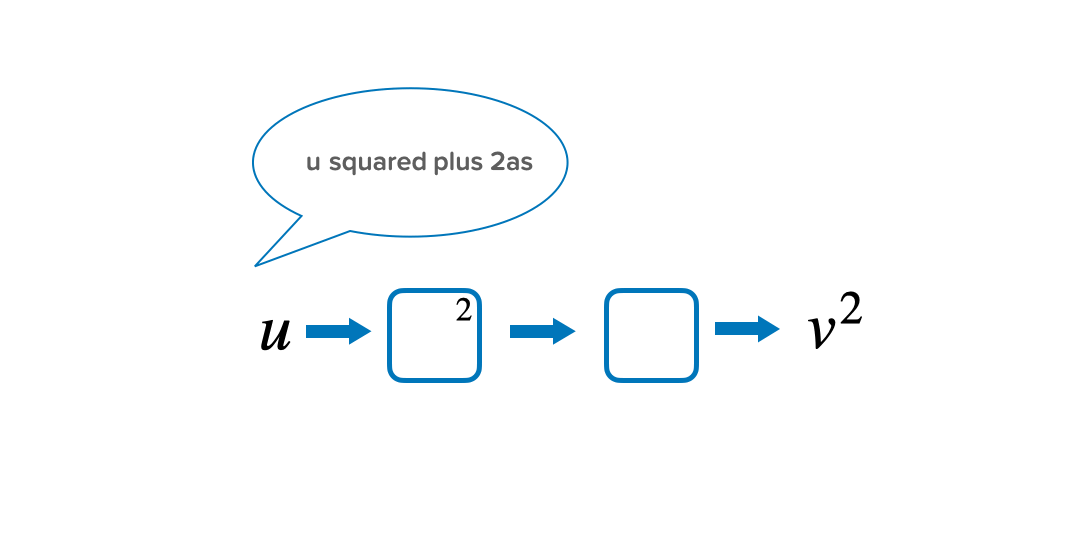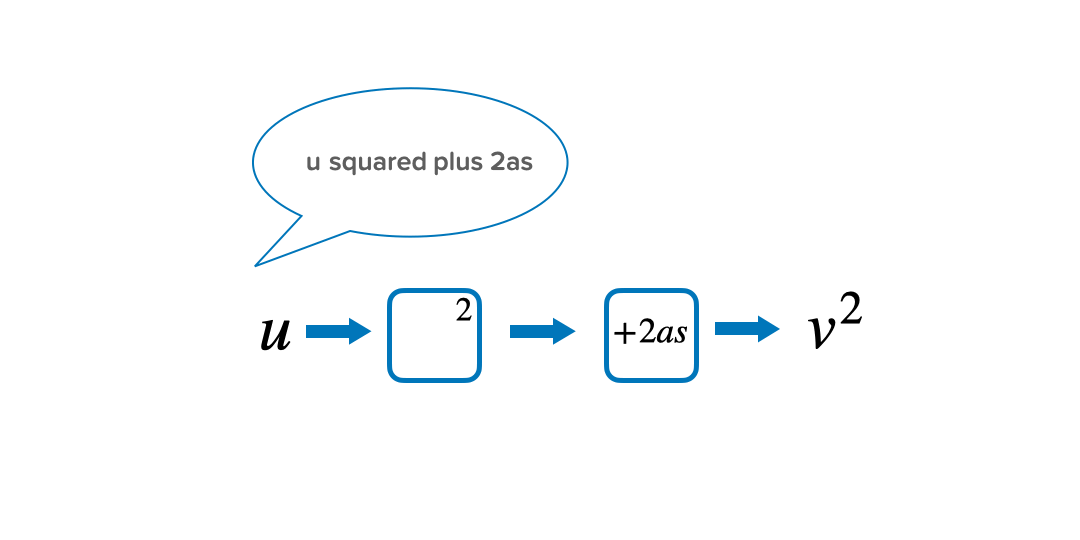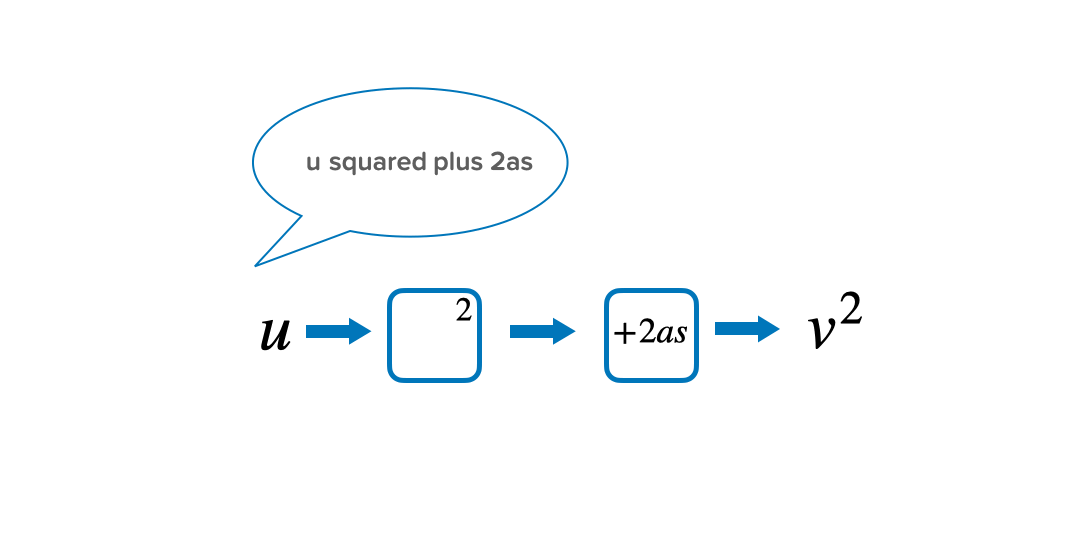
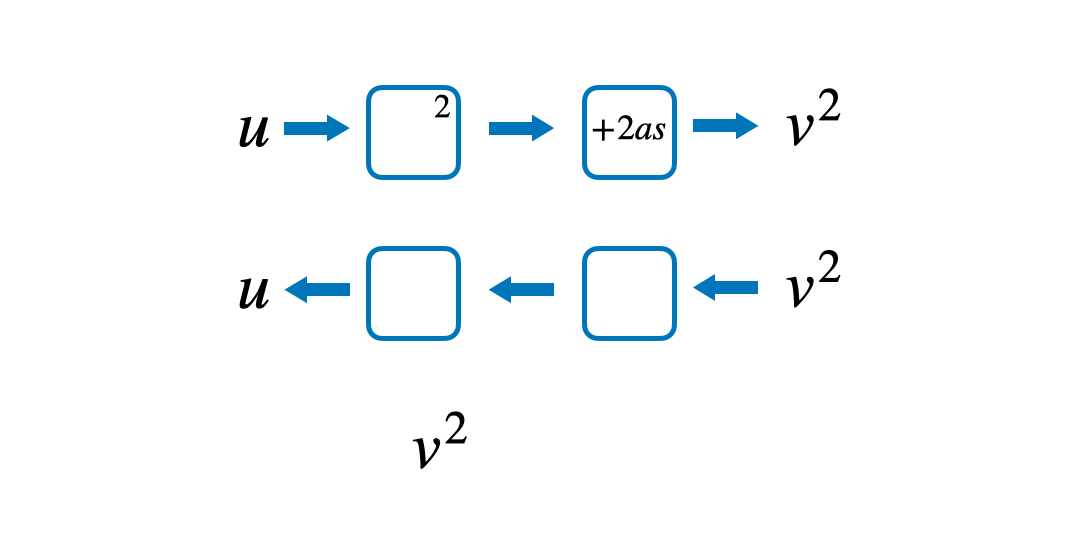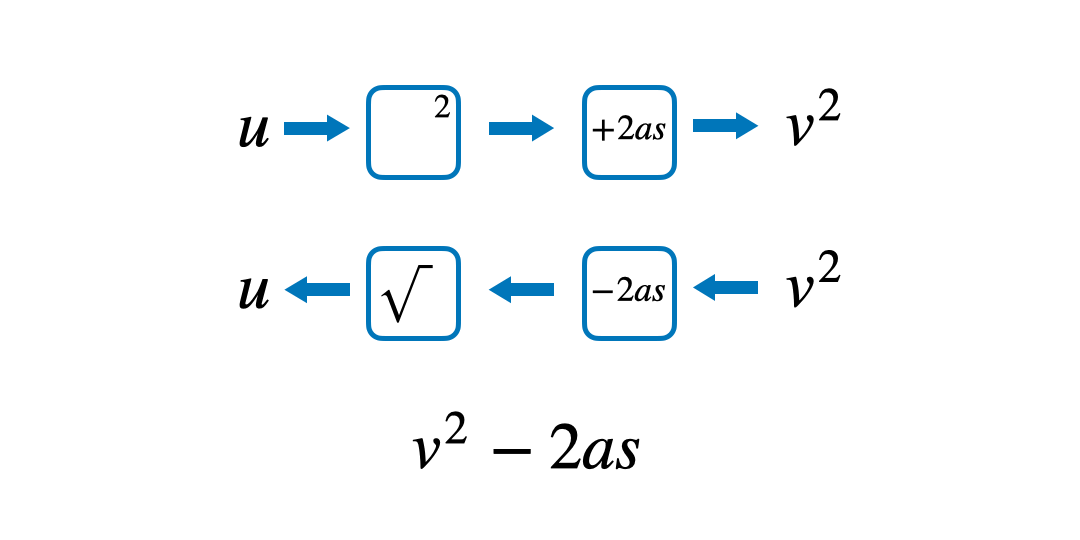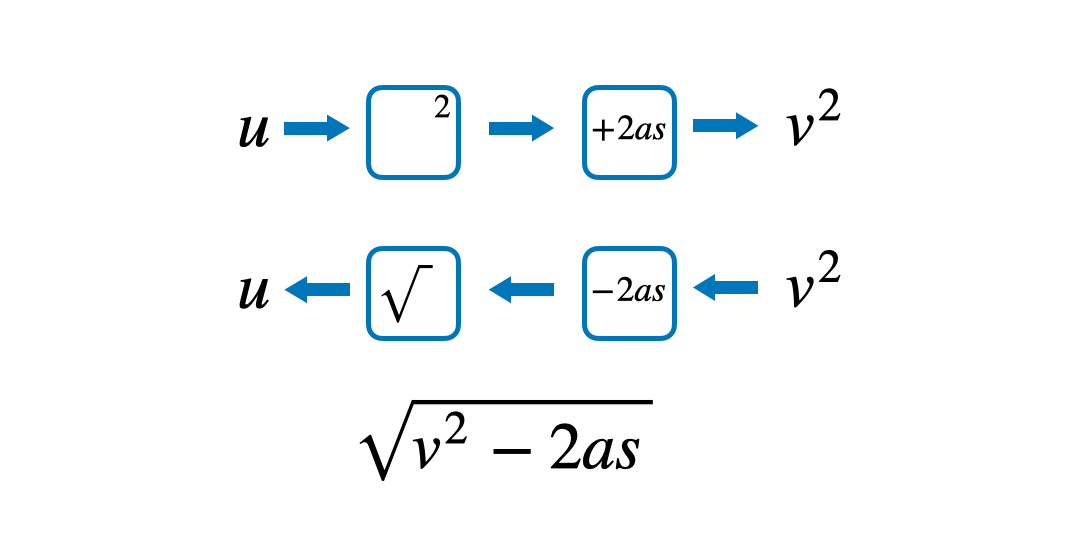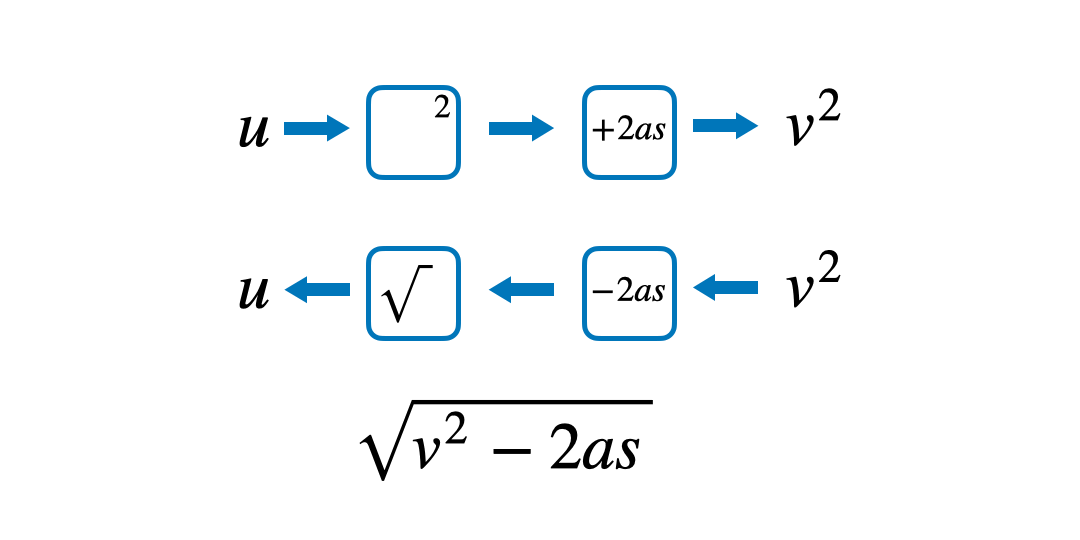
Quite often students find it hard to understand in what order the operations have happened. By saying the formula out loud and writing these steps down in a function machine, it can be easier to follow the steps to prevent confusion. Starting with the variable that they want to make the subject, read out the formula to answer the question ‘what has happened to u to get v^2?’
Then, implement knowledge of inverse operations to work backwards to make u the subject.
We hope that this blog gives you an insight into some of the common challenges learners face when rearranging formulae, and our practical teaching ideas help boost your learners’ confidence and understanding.
Look at the data on your Teacher Dashboard to see if these common misconceptions are present among your learners. Book a demo here.