Estimated reading time: 6 minutes
The idea of variation theory is “to highlight the essential features of the concept through varying the non-essential features”. This aims to help learners think more critically about concepts and be able to apply them in a wider range of contexts.
There are two types of variation theory that are going to be explored in this blog post: conceptual variation and procedural variation.
Conceptual variation
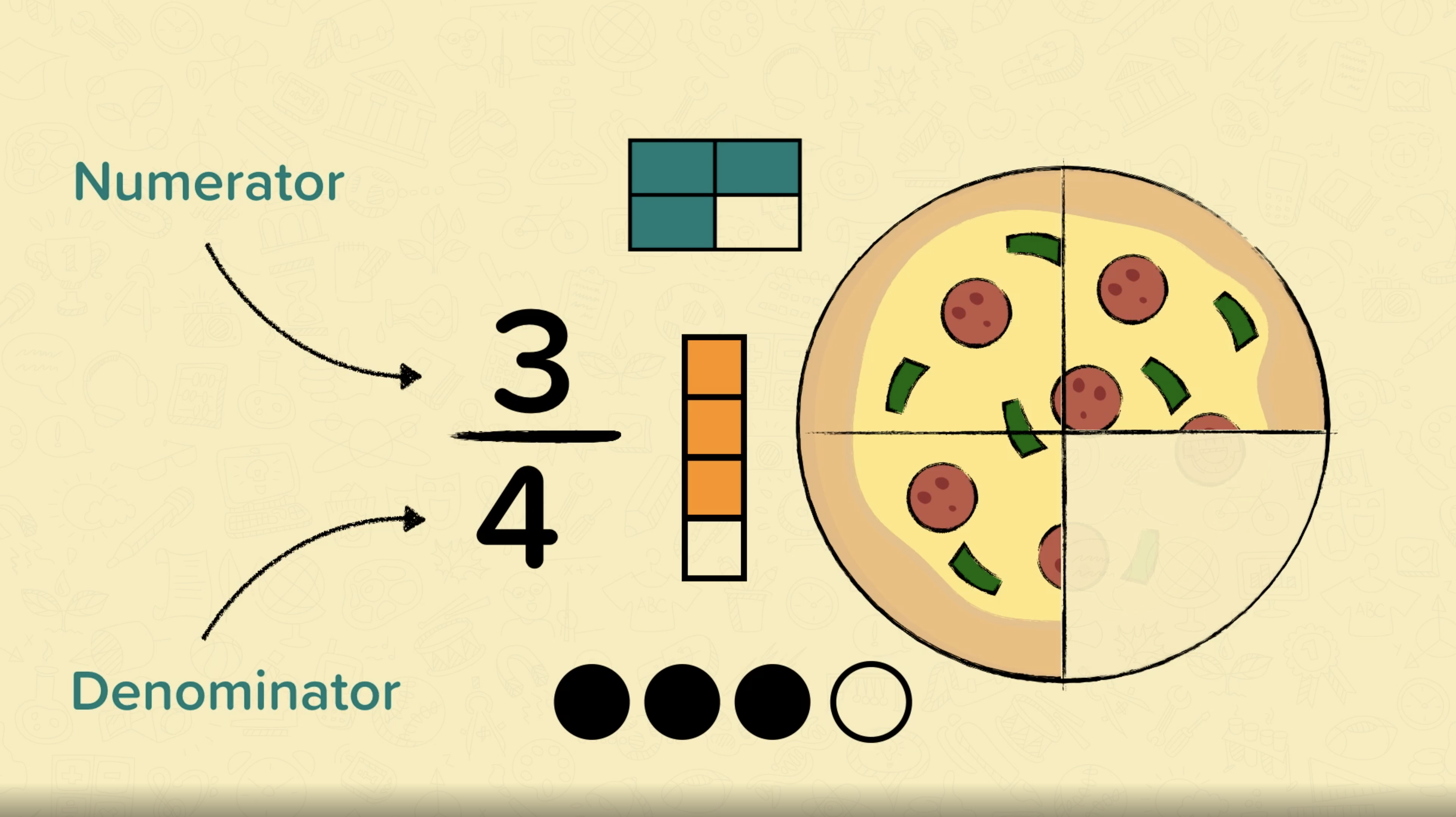
Conceptual variation involves showing learners different representations of the same concept in order to deepen their understanding of it. Below, for example, you can see that alongside the fraction ¾, there are four visual representations.
This helps students to see that although the representations are different, they all represent 3 out of 4. They can then start to understand that fractions are not just a mathematical concept, but something that can be understood in the real world.
Similarly, if you look at the image below, you will notice that the four shapes presented are all hexagons. Although only the one on the far left is a regular hexagon, all the representations are of different sizes and different colours, have sides of different lengths, and having differing orientations, they all classify as hexagons. This shows learners that a hexagon can be represented in a lot of different ways.
In the image below, there is also one shape that is not a hexagon. Asking pupils to identify which shape that is encourages them to think more deeply about what exactly constitutes a hexagon, reinforcing the idea that while a hexagon doesn’t need to be of a certain colour or size, it must have six straight sides.
When applying conceptual variation, it is important to include standard examples, non-standard examples and ‘odd ones out’ to help learners develop a more rounded understanding of the concept being taught.
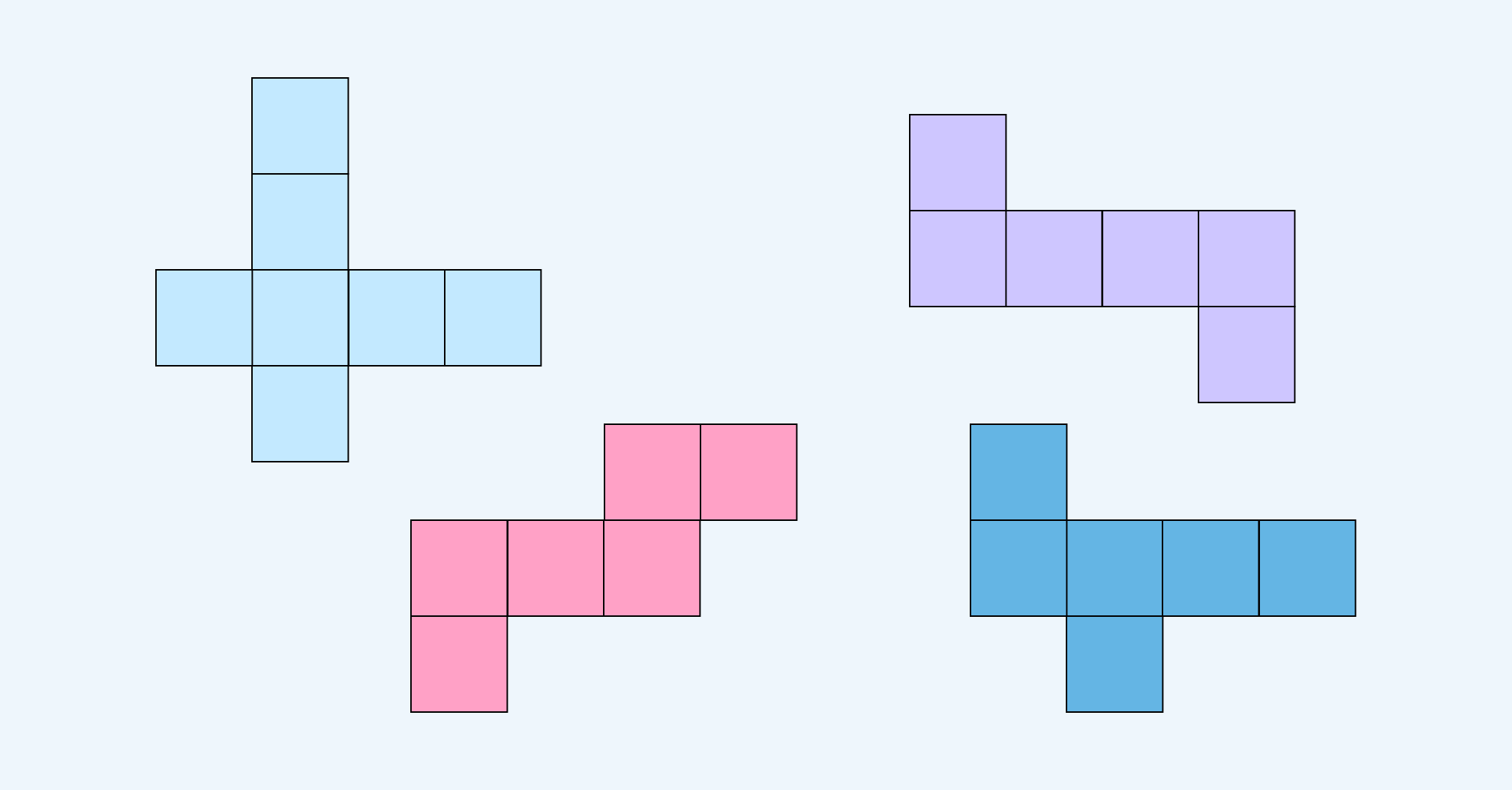
One question that often trips children up is identifying a cube and its net. The classic net that most pupils can easily recognise is the T shape, but there are 11 different nets that a cube could have, and students need to be able to recognise all of them.
They also need to know how to spot when a net could not make a cube – for example, the top left net below could not make a cube because it has seven faces. By recognising this, the idea is reinforced that a cube must have six faces.
Variation theory is often useful for teaching visual concepts, but it can be used for other purposes as well. We can apply a similar logic to vary the way we set out questions, for example, by presenting multiplication questions as ‘?=5x7’ as well as ‘5x7=?’ to help learners better understand what ‘=’ really is: a symbol of mathematical equivalence, not an operational symbol.
Procedural variation
Procedural variation involves slightly varying the concept that is being taught from one question to the next while keeping everything else the same, allowing learners to build on their previous knowledge step by step. By being encouraged to identify what is the same and what has changed, learners' conceptual thinking skills are exercised.
If you look at the two sets of questions below, you can guess which was designed with procedural variation in mind.
The answer is A. The first question requires the learner to find ⅓ of 12, the second to find ⅔ of 12, and the third to find ⅔ of 24. This encourages students to use reasoning to make links between the questions. Once they’ve figured out that a ⅓ of 12 is 4, they can multiply their answer by two to answer the second question. Then, realising that 24 is double 12, they can double their answer to the second question to find the answer to the third question.
In addition to improving their fluency in answering questions on fractions, this use of procedural variation helps to develop the learner’s reasoning and conceptual thinking skills.
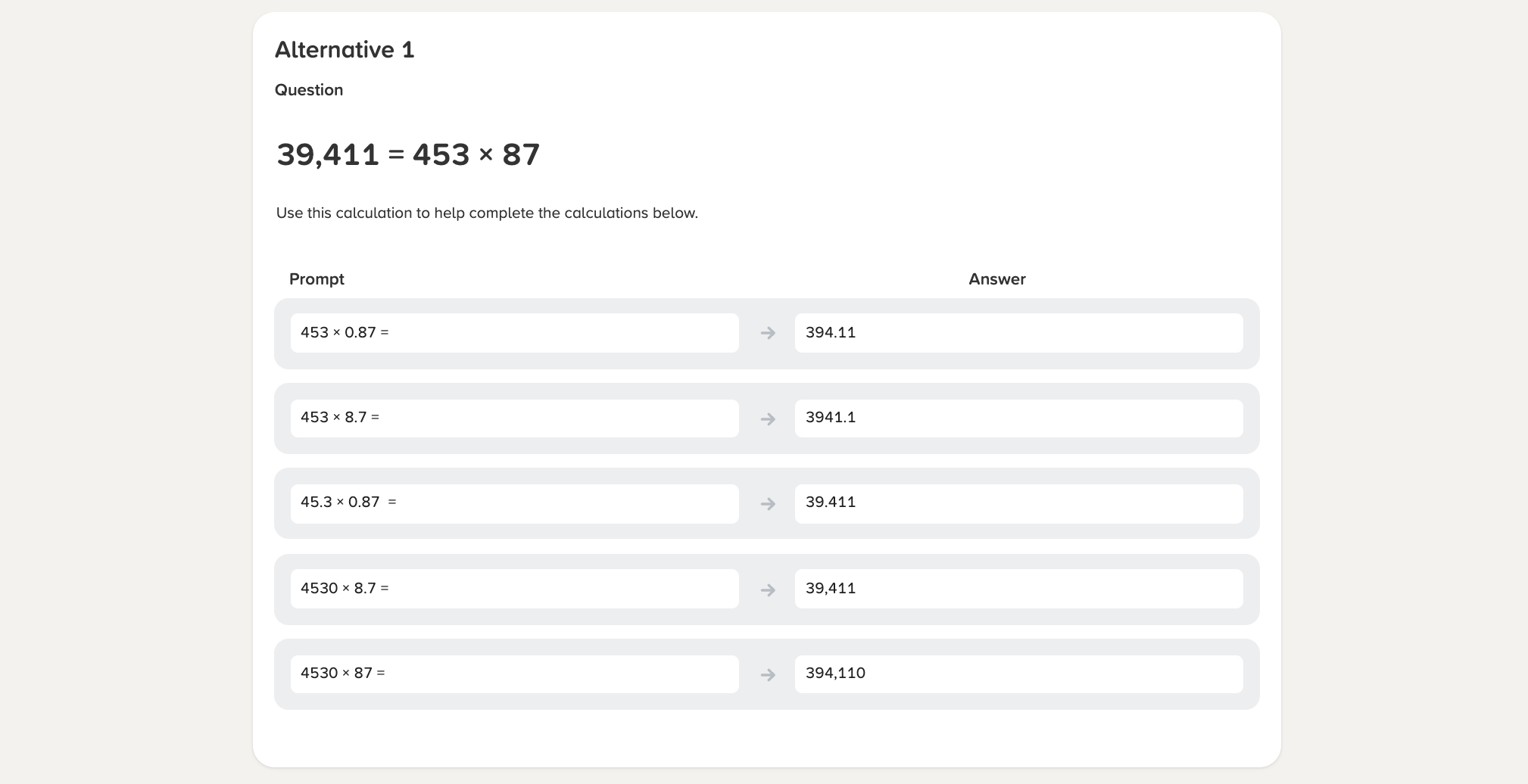
There are various ways that this could be presented. In the question below, for example, students are given one calculation and explicitly prompted to use it to solve three related calculations.
When implementing procedural variation, it is important to note that the accompanying dialogue is as important as question design.
Encouraging students to explain aloud what they understand about the relationship between each question as they go will help ensure that they are building links between questions rather than tackling each question independent of each other.
Book a demo to find out more about how CENTURY can help to enhance the teaching and learning at your school or college.